The Importance of Representation
Throughout the years, I was not taught to think about representations when solving problems. The standard problem-solving framework I used never consciously considered changing the inputs of problems to better suit the desired outcome.
During the past year, I realized that choosing the suitable representation of a problem can be the difference between a nightmare and a breeze.
Usually, when faced with a problem or a situation, it is easy for us to receive it as presented. We try to find a solution to the exact way the issue is raised to us.
A change in representation allows us to think differently about the solution to our problem.
A famous quote often attributed to Henry Ford, "If I had asked people what they wanted, they would have said faster horses." highlights the cognitive ease humans tend to prefer when faced with an issue.
When examining faster transportation, most people default to the existing tools and solutions, making them ever so slightly better than before. They would try to find ways to make the horses stronger and quicker which is a good school of thought and has its place.
Yet, from time to time, it is essential to remove all restrictions and beliefs we have for a problem and a solution, think only of the fundamental principles that govern the problem, no additional assumptions.
When reducing faster transportation to the fundamentals, it becomes clear that it is not tied to existing transportation tools. We are free to examine other devices such as motorized vehicles.
Let us take a familiar example, a change in representation that might have gone unnoticed by most of us - water handles.
When I was a child, all water facets had two handles, one for cold water and the other for hot water. When stepping into people's shoes in the past, it is easy to understand why two handles exist - the plumbing in our home has a pipeline for cold water and hot water. It is very reasonable and straightforward to expose these pipes in the form of two handles.
Still, if we take a moment to think of the inputs and outputs, the following is apparent.
As long as we do not intend to change our home's piping system, hot and cold water are the inputs. Temperature seems like the only output at first glance, but a hidden variable reveals itself, pressure. The larger the input is from any pipeline, the larger the pressure is.
When using a water faucet, we desire water at a specific pressure and temperature. When using a two-handle system, it is very tricky to accomplish. Adjusting the temperature (one handle) inevitably changes the water pressure and vice-versa.
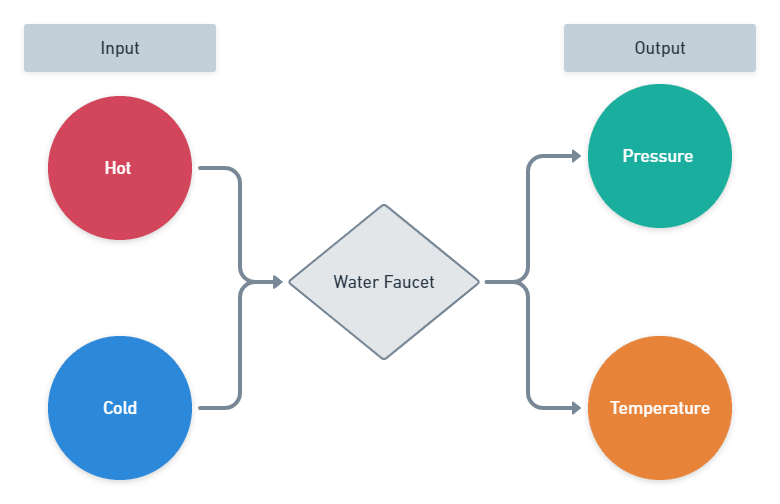
Throughout the years, a solution to the problem emerged - a lever. A change to the representation of inputs, instead of hot and cold handles, temperature and pressure handles are exposed.
This change now allows us to change the temperature without pressure and gives us complete control over the output.

Although this example might seem obvious, the idea behind the change is valuable to remember and can be applied to all aspects of our lives.
I find myself using it when solving theoretical problems in my thesis, writing code, making difficult personal decisions, and much more.
Knowing how to represent a problem is a powerful thinking model. When stuck with a problem, try to reduce its fundamental components - inputs and outputs, decide on the most crucial output.
Choose the best representation of inputs such that the desired result is easy to control.
Next time you face a problem, take a few moments to break it down. Even if you don't find a better representation, you will most likely find new insights.